Statistics with SciPy, Statsmodels, and Pingouin
Libraries for statistics
SciPy
SciPy is a Python package with a large number of functions for numerical computing. It also contains statistical functions, but only for basic statistical tests (t-tests etc.).
Statsmodels
More advanced statistical tests are provided by Statsmodels. Statsmodels is powerful, but not very user-friendly; therefore, the tutorial below shows examples of several commonly used statistical tests.
Pingouin
Pingouin is a relatively new Python library for statistics. It provides more uniform and user-friendly functions than SciPy and Statsmodels.
Example datasets
All datasets used below are taken from the example data included with JASP, with the exception of the Zhou et al. (2020) dataset used for the Repeated Measures ANOVA.
T-tests
Independent-samples t-test
Consider this dataset from Matzke et al. (2015). In this dataset, participants performed a memory task in which they recalled a list of words. During the retention interval, one group of participants looked at a central fixation dot on a display. Another group of participants continuously made horizontal eye movements, which is believed by some to improve memory.
You can use the ttest_ind() function from scipy.stats to test whether memory performance (CriticalRecall) was higher for the horizontal-eye-movement group as compared to the fixation group.
from datamatrix import io, operations as ops
from scipy.stats import ttest_ind
dm = io.readtxt('data/matzke_et_al.csv')
dm_horizontal, dm_fixation = ops.split(dm.Condition, 'Horizontal', 'Fixation')
t, p = ttest_ind(dm_horizontal.CriticalRecall, dm_fixation.CriticalRecall)
print('t = {:.4f}, p = {:.4f}'.format(t, p))
Output:
t = -2.8453, p = 0.0066
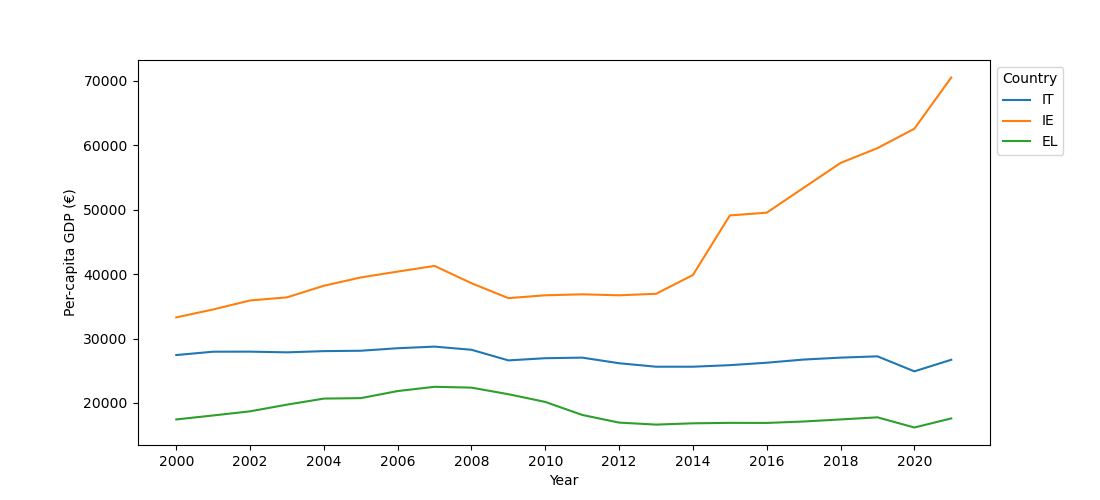
This reveals a significant difference (p = .0066). However, as you can see in the figure below, the effect goes in the opposite direction from the prediction, such that the fixation group performed best.
You can also use the ttest() function from pingouin. This also provides a Bayes Factor, for those who are into Bayesian statistics.
import pingouin as pg
df = pg.ttest(dm_horizontal.CriticalRecall, dm_fixation.CriticalRecall)
print(df)
Output:
T dof alternative p-val CI95% cohen-d BF10 power
T-test -2.823413 40.268769 two-sided 0.007352 [-7.57, -1.25] 0.813105 6.455 0.795808
It's always helpful to visualize the results:
from matplotlib import pyplot as plt
import seaborn as sns
sns.barplot(x='Condition', y='CriticalRecall', data=dm)
plt.xlabel('Condition')
plt.ylabel('Memory performance')
plt.show()
Output:
/home/sebastiaan/anaconda3/envs/pydata/lib/python3.10/site-packages/outdated/utils.py:14: OutdatedPackageWarning: The package pingouin is out of date. Your
version is 0.5.3, the latest is 0.5.4.
Set the environment variable OUTDATED_IGNORE=1 to disable these warnings.
return warn(
[32m⠏[0m Generating...
Paired-samples t-test
Consider this dataset from Moore, McCabe, & Craig. Here, aggressive behavior from people suffering from dementia was measured during full moon and another phase of the lunar cycle. Each participant was measured at both phases, i.e. this was a within-subject design.
You can use the ttest_rel() function to test whether aggression differed between the full moon and the other lunar phase.
from datamatrix import io
from scipy.stats import ttest_rel
dm = io.readtxt('data/moon-aggression.csv')
t, p = ttest_rel(dm.Moon, dm.Other)
print('t = {:.4f}, p = {:.4f}'.format(t, p))
Output:
t = 6.4518, p = 0.0000
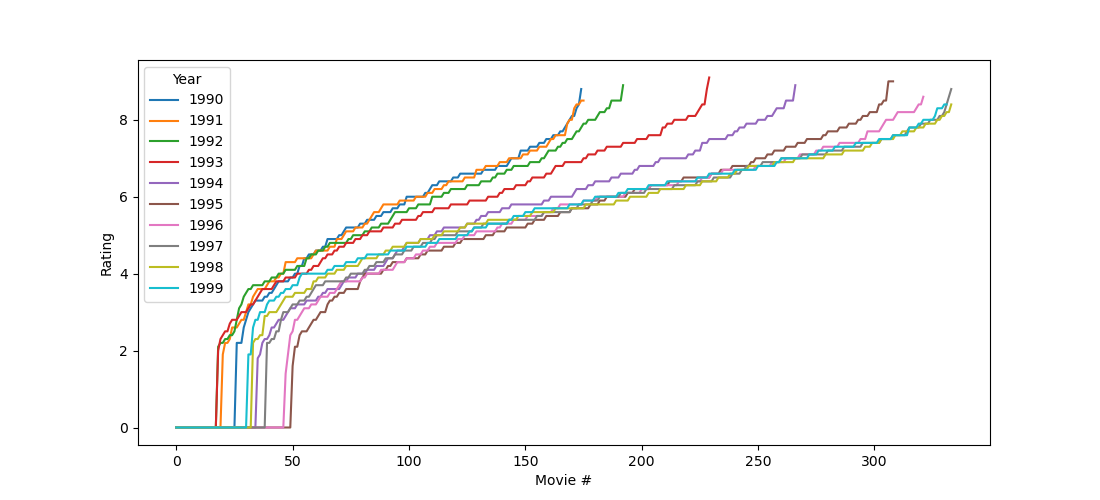
Interestingly, there was indeed a significant effect (p < .0001; note that p values are never 0 as the output implies!), and this effect was in such that people were indeed most aggressive during full moon, as you can see in the figure below.
You can also use the ttest() function from pingouin and use the paired keyword to indicate that this is a paired-samples t-test, as opposed to an independent-samples t-test.
import pingouin as pg
df = pg.ttest(dm.Moon, dm.Other, paired=True)
print(df)
Output:
T dof alternative p-val CI95% cohen-d BF10 power
T-test 6.451789 14 two-sided 0.000015 [1.62, 3.24] 2.200516 1521.058 1.0
And let's visualize the result. Because the measurements of the data are in two separate columns, we cannot easily use Seaborn for plotting. But we can resort to a quick plot with plt.plot().
from matplotlib import pyplot as plt
plt.plot([dm.Moon.mean, dm.Other.mean], 'o-')
plt.xticks([0, 1], ['Moon', 'Other'])
plt.ylabel('Aggression')
plt.xlabel('Lunar phase')
plt.show()
One-sample t-test
If we take the difference between the Moon and Other measurements of the above dataset, then we can test this difference against zero (or another value specified with the popmean keyword) with ttest_1samp():
from datamatrix import io
from scipy.stats import ttest_1samp
dm = io.readtxt('data/moon-aggression.csv')
diff = dm.Moon - dm.Other
t, p = ttest_1samp(diff, popmean=0)
print('t = {:.4f}, p = {:.4f}'.format(t, p))
Output:
t = 6.4518, p = 0.0000
You can also use the ttest() function from pingouin. To indicate that this is a one-sample t-test against zero, simply pass 0 as the second argument.
import pingouin as pg
df = pg.ttest(diff, 0)
print(df)
Output:
T dof alternative p-val CI95% cohen-d BF10 power
T-test 6.451789 14 two-sided 0.000015 [1.62, 3.24] 1.665845 1521.058 0.999969
Regression
Correlation / simple linear regression
This dataset, taken from Rotten Tomatoes, contains the 'freshness' rating and the Box Office profit for all of Adam Sandler's movies. You can use linregress() from scipy.stats to test if highly rated Adam Sandler movies make more money than poorly rated ones.
from datamatrix import io
from scipy.stats import linregress
dm = io.readtxt('data/adam-sandler.csv')
slope, intercept, r, p, se = linregress(dm.Freshness, dm['Box Office ($M)'])
print('Box Office = {:.2f} * Freshness + {:.2f}'.format(slope, intercept))
print('p = {:.4f}, r = {:.4f}'.format(p, r))
Output:
Box Office = -7.08 * Freshness + 80.13
p = 0.8785, r = -0.0286
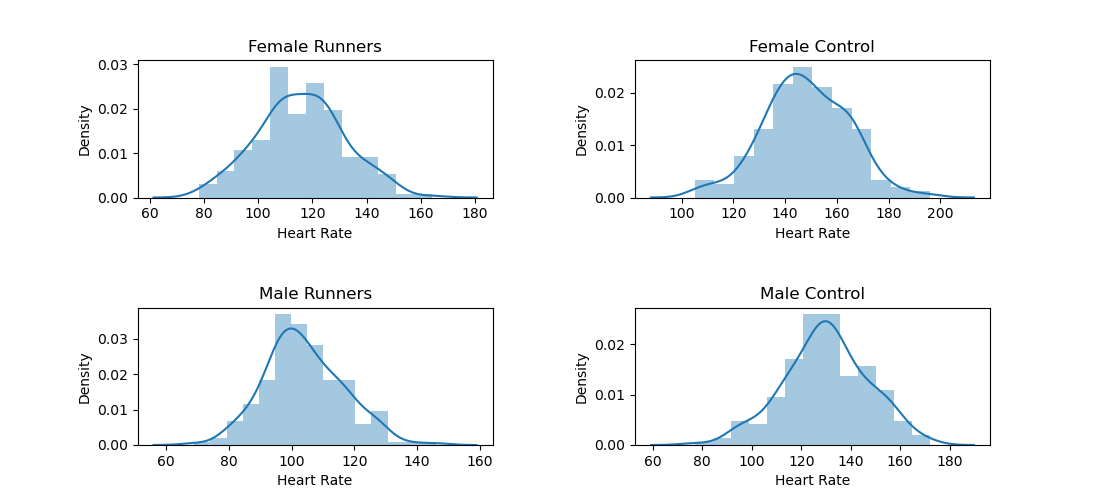
There seems to be no notable relationship between the freshness ratings of Adam Sandler's movies and their Box Office profit (p = .8785), as you can also see in the figure below.
You can also use the linear_regression() function from pingouin. Here, the intercept and slope simply correspond to the first and second values in the coef column.
import pingouin as pg
df = pg.linear_regression(X=dm.Freshness, y=dm['Box Office ($M)'])
print(df)
Output:
names coef se T pval r2 adj_r2 CI[2.5%] CI[97.5%]
0 Intercept 80.131114 15.414851 5.198306 0.000015 0.00082 -0.033634 48.604203 111.658025
1 x1 -7.077644 45.872789 -0.154288 0.878451 0.00082 -0.033634 -100.898031 86.742744
To get the correlation, you can use the corr function from pingouin.
df = pg.corr(dm.Freshness, dm['Box Office ($M)'])
print(df)
Output:
n r CI95% p-val BF10 power
pearson 31 -0.028639 [-0.38, 0.33] 0.878451 0.226 0.052211
To visualize this relationship, you can use Seaborn's regplot() function.
from matplotlib import pyplot as plt
import seaborn as sns
sns.regplot(x='Freshness', y='Box Office ($M)', data=dm)
plt.show()
Multiple linear regression
Consider this dataset from Moore, McCabe, & Craig which contains grade-point averages (gpa) and SAT scores for mathematics (satm) and verbal knowledge (satv) for 500 high-school students. To test whether satm and satv are (uniquely) related to gpa, you can use the code below.
The series of function calls (model = ols(…).fit() and then model.summary()) isn't very elegant, but the important part is the formula that is specified in a string with an R-style formula.
from datamatrix import io
from statsmodels.formula.api import ols
dm = io.readtxt('data/gpa.csv')
model = ols('gpa ~ satm + satv', data=dm).fit()
print(model.summary())
Output:
OLS Regression Results
==============================================================================
Dep. Variable: gpa R-squared: 0.063
Model: OLS Adj. R-squared: 0.055
Method: Least Squares F-statistic: 7.476
Date: do, 09 mei 2024 Prob (F-statistic): 0.000722
Time: 11:38:46 Log-Likelihood: -254.18
No. Observations: 224 AIC: 514.4
Df Residuals: 221 BIC: 524.6
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 1.2887 0.376 3.427 0.001 0.548 2.030
satm 0.0023 0.001 3.444 0.001 0.001 0.004
satv -2.456e-05 0.001 -0.040 0.968 -0.001 0.001
==============================================================================
Omnibus: 23.688 Durbin-Watson: 1.715
Prob(Omnibus): 0.000 Jarque-Bera (JB): 27.838
Skew: -0.809 Prob(JB): 9.02e-07
Kurtosis: 3.601 Cond. No. 5.85e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 5.85e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
This reveals that only SAT scores for mathematics (t = 3.444, p = .001), but not for verbal knowledge (t = -0.040, p = .968), are uniquely related to grade point average.
You can also use the linear_regression() function from pingouin. The first argument, X, now consists of multiple columns (as opposed to a single column when doing a simple linear regression). To select the columns that should be used as predictors, you can simply select them directly from the datamatrix (dm['satm', 'satv']).
import pingouin as pg
df = pg.linear_regression(X=dm['satm', 'satv'], y=dm.gpa)
print(df)
Output:
names coef se T pval r2 adj_r2 CI[2.5%] CI[97.5%]
0 Intercept 1.288677 0.376037 3.426998 0.000728 0.063367 0.05489 0.547600 2.029754
1 x1 0.002283 0.000663 3.443634 0.000687 0.063367 0.05489 0.000976 0.003589
2 x2 -0.000025 0.000618 -0.039714 0.968357 0.063367 0.05489 -0.001243 0.001194
ANOVA
ANOVA (regular)
Let's go back to this heart-rate data from Moore, McCabe, and Craig. This dataset contains two factors that vary between subjects (Gender and Group) and one dependent variable (Heart Rate). To test whether Gender, Group, or their interaction affect heart rate, you need the following code.
As above, the combination of ols() and anova_lm() isn't very elegant, but the important part is the formula.
from datamatrix import io
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
dm = io.readtxt('data/heartrate.csv')
dm.rename('Heart Rate', 'HeartRate') # statsmodels doesn't like spaces
df = anova_lm(ols('HeartRate ~ Gender * Group', data=dm).fit())
print(df)
Output:
df sum_sq mean_sq F PR(>F)
Gender 1.0 45030.005 45030.005000 185.979949 3.287945e-38
Group 1.0 168432.080 168432.080000 695.647040 1.149926e-110
Gender:Group 1.0 1794.005 1794.005000 7.409481 6.629953e-03
Residual 796.0 192729.830 242.122902 NaN NaN
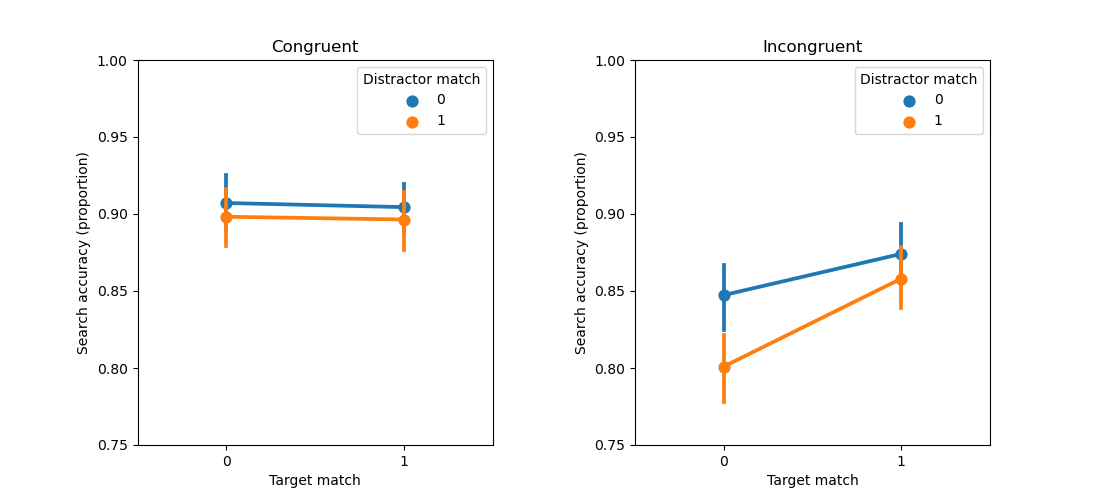
This reveals that heart rate is related to all factors: gender (F = 185.980, p < .001), group (F = 695.647, p < .001), and the gender-by-group interaction (F = 7.409, p = .006).
You can also use the anova function from pingouin.
import pingouin as pg
aov = pg.anova(dv='HeartRate', between=['Gender', 'Group'], data=dm)
print(aov)
Output:
Source SS DF MS F p-unc np2
0 Gender 45030.005 1 45030.005000 185.979949 3.287945e-38 0.189393
1 Group 168432.080 1 168432.080000 695.647040 1.149926e-110 0.466362
2 Gender * Group 1794.005 1 1794.005000 7.409481 6.629953e-03 0.009223
3 Residual 192729.830 796 242.122902 NaN NaN NaN
You can visualize this result with Seaborn:
from matplotlib import pyplot as plt
import seaborn as sns
sns.pointplot(x='Group', y='HeartRate', hue='Gender', data=dm)
plt.xlabel('Group')
plt.ylabel('Heart rate')
plt.show()
Repeated Measures ANOVA
A Repeated Measures ANOVA is generally used to analyze data from experiments in which all participants take part in all conditions, that is, a within-subject design. An example of such a design comes from an experiment by Zhou and colleagues, in which participants searched for a target object in the presence of a distractor object. Either the target, or the distractor, or both could match a color that participants held in memory. You can download this dataset here.
To test whether the factors distractor-match, target-match, and their interaction affect search accuracy, you can use the AnovaRM class from statsmodels.stats.anova.
Somewhat different most other RM-ANOVA software, the AnovaRM class accepts the data in long, unaggregated format. That is, each row corresponds to a single observation. Statsmodels will automatically reduce this format to a format where observations are aggregated per participant and condition (which is the required format for an RM-ANOVA) using the method indicated with the aggregate_func keyword:
from datamatrix import io
from statsmodels.stats.anova import AnovaRM
dm = io.readtxt('data/zhou_et_al_2020_exp1.csv')
aov = AnovaRM(
dm,
depvar='search_correct',
subject='subject_nr',
within=['target_match', 'distractor_match'],
aggregate_func='mean'
).fit()
print(aov)
Output:
Anova
===========================================================
F Value Num DF Den DF Pr > F
-----------------------------------------------------------
target_match 6.7339 1.0000 34.0000 0.0139
distractor_match 13.9729 1.0000 34.0000 0.0007
target_match:distractor_match 7.1687 1.0000 34.0000 0.0113
===========================================================
This reveals that search accuracy is affected by all factors: target match (F = 6.7339, p = .0139), distractor match (F = 13.9729, p = .0007), and the target match by distractor match interaction (F = 7.1687, p = .0113).
You can also use the rm_anova function from pingouin.
import pingouin as pg
aov = pg.rm_anova(
dv='search_correct',
within=['target_match', 'distractor_match'],
subject='subject_nr',
data=dm
)
print(aov)
Output:
Source SS ddof1 ddof2 MS F p-unc p-GG-corr ng2 eps
0 target_match 0.013813 1 34 0.013813 6.733860 0.013863 0.013863 0.002314 1.0
1 distractor_match 0.013813 1 34 0.013813 13.972917 0.000681 0.000681 0.002314 1.0
2 target_match * distractor_match 0.002136 1 34 0.002136 7.168675 0.011339 0.011339 0.000359 1.0
Let's visualize this result.
We could (but shouldn't!) simply create a pointplot based on dm. But this plot would not take into account that a Repeated Measures ANOVA is based on aggregated data (i.e. one observation per condition and participant). And therefore the error bars of this plot would not reflect the variation between participants (as it should), but rather the variation between individidual trials.
To make a more appropriate figure, we first use ops.group() to create a new datamatrix, gm, in each row corresponds to a single condition for a single participant. Initially, gm.search_correct then corresponds to a series of values, one for each trial. (It is a SeriesColumn, a powerful type of column about which you can read more here.) We use srs.reduce_() to change this series of values to a single, mean value. Finally, we remove the between-subject variability, which is a fancy way of saying that we change search_correct such that it is on average the same for each participant, without changing the overall average of search_correct across participants. (This procedure is described in more detail in this blogpost.)
And then we can finally create a plot that is an appropriate match to the Repeated Measures ANOVA!
from matplotlib import pyplot as plt
import seaborn as sns
from datamatrix import operations as ops, series as srs
# Group the data by condition and subject
gm = ops.group(
dm,
by=[dm.target_match, dm.distractor_match, dm.subject_nr]
)
gm.search_correct = srs.reduce_(gm.search_correct)
# Remove between-subject variability
for subject_nr, sm in ops.split(gm.subject_nr):
gm.search_correct[sm] = sm.search_correct - sm.search_correct.mean + gm.search_correct.mean
# And plot!
sns.pointplot(
x='target_match',
y='search_correct',
hue='distractor_match',
data=gm
)
plt.xlabel('Target match')
plt.ylabel('Search accuracy (proportion)')
plt.legend(title='Distractor match')
plt.show()
Tip: If you prefer to conduct the RM-ANOVA with different software, such as JASP or SPSS, then you first need to create a so-called pivot table, in which each row corresponds to a subject, and each column to a condition. You can do this with the ops.pivot_table() function:
pm = ops.pivot_table(
dm,
values=dm.search_correct,
index=dm.subject_nr,
columns=[dm.target_match, dm.distractor_match]
)
print(pm)
Output:
+----+----------+----------+----------+----------+
| # | 0_0 | 0_1 | 1_0 | 1_1 |
+----+----------+----------+----------+----------+
| 0 | 0.96875 | 0.921875 | 1 | 0.953125 |
| 1 | 1 | 0.96875 | 1 | 0.9375 |
| 2 | 1 | 0.9375 | 1 | 0.984375 |
| 3 | 1 | 0.953125 | 0.96875 | 0.96875 |
| 4 | 0.921875 | 0.859375 | 1 | 0.953125 |
| 5 | 0.984375 | 0.96875 | 0.984375 | 1 |
| 6 | 1 | 1 | 1 | 1 |
| 7 | 0.96875 | 0.96875 | 0.984375 | 1 |
| 8 | 1 | 0.984375 | 1 | 0.984375 |
| 9 | 1 | 0.984375 | 1 | 1 |
| 10 | 0.015625 | 0.03125 | 0 | 0 |
| 11 | 0.984375 | 0.9375 | 0.984375 | 0.953125 |
| 12 | 0.90625 | 0.84375 | 0.953125 | 0.953125 |
| 13 | 0.9375 | 0.984375 | 0.953125 | 0.96875 |
| 14 | 0.828125 | 0.8125 | 0.84375 | 0.8125 |
| 15 | 0.953125 | 0.921875 | 1 | 0.984375 |
| 16 | 0.890625 | 0.84375 | 0.90625 | 0.890625 |
| 17 | 0.984375 | 0.96875 | 0.96875 | 0.96875 |
| 18 | 0.578125 | 0.484375 | 0.5 | 0.515625 |
| 19 | 0.5 | 0.5625 | 0.484375 | 0.5625 |
+----+----------+----------+----------+----------+
(+ 15 rows not shown)
Linear mixed-effects modeling
A linear mixed-effects model (or: linear mixed-effects regression) is a modern statstical-analysis technique for 'hierarchical' datasets. This sounds complicated, but the most common type of hierarchy is simply a dataset that consists of multiple observations from multiple participants. The Zhou et al. dataset, described above, is an example of such a dataset.
In many cases, you can analyze the same dataset using either a Repeated Measures ANOVA or a linear mixed-effects model; however, one crucial difference is that a Repeated Measures ANOVA requires you to aggregate data across multiple observations (e.g. by calculating the mean reaction time per participant and condition), whereas a linear mixed-effects model is performed on unaggregated data, i.e. on individual observations. In addition, linear mixed-effects modeling offers far more flexibility for analyzing complex datasets that you cannot analyze with a Repeated Measures ANOVA.
Let's say that we want to analyze search reaction times as a function of the conditions target match and distractor match, and that we want to have random by-participant intercepts and slopes. The most well-known package for linear mixed-effects modeling is the R package lme4, in which case this analysis corresponds to the formula:
search_rt ~ target_match * distractor_match + (1 + target_match * distractor_match | subject_nr)
In Python, we need to use statsmodels for this, and the syntax is slightly different. Notably, the random effects structure is passed separately as the re_formula keyword:
from datamatrix import io
from statsmodels.formula.api import mixedlm
dm = io.readtxt('data/zhou_et_al_2020_exp1.csv')
model = mixedlm(formula='search_rt ~ target_match * distractor_match',
re_formula='~ target_match * distractor_match',
data=dm, groups='subject_nr').fit()
print(model.summary())
Output:
Mixed Linear Model Regression Results
=======================================================================================================
Model: MixedLM Dependent Variable: search_rt
No. Observations: 8960 Method: REML
No. Groups: 35 Scale: 105803.2305
Min. group size: 256 Log-Likelihood: -64683.5652
Max. group size: 256 Converged: Yes
Mean group size: 256.0
-------------------------------------------------------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------------------------------
Intercept 1056.900 64.632 16.353 0.000 930.223 1183.577
target_match -113.602 17.267 -6.579 0.000 -147.444 -79.759
distractor_match 60.356 11.541 5.230 0.000 37.736 82.976
target_match:distractor_match 47.132 18.910 2.492 0.013 10.070 84.195
subject_nr Var 144553.219 109.235
subject_nr x target_match Cov -1867.445 20.680
target_match Var 7128.699 7.796
subject_nr x distractor_match Cov -3217.240 14.003
target_match x distractor_match Cov -2778.028 3.725
distractor_match Var 1355.484 3.482
subject_nr x target_match:distractor_match Cov 2470.514 22.659
target_match x target_match:distractor_match Cov -109.659 6.291
distractor_match x target_match:distractor_match Cov 377.434 4.315
target_match:distractor_match Var 5902.857 9.349
=======================================================================================================
This reveals that search reaction times are affected by all factors: target match (z = -6.579, p < .001), distractor match (z = 5.230, p < .001), and the target match by distractor match interaction (z = 2.492, p = .013).
Exercises
A three-way Repeated Measures ANOVA
Above you have seen how to conduct a two-way repeated measures ANOVA with this dataset from Zhou et al. (2020). But the data contains a third factor: congruency. First, run a three-way repeated measures ANOVA with target-match, distractor-match, and congruency as independent variables, and search accuracy as dependent variable. Next, plot the results in a two-panel plot, where the left subplot shows the effect of distractor and target match for congruent trials, while the right subplot shows this for incongruent trials.
Correlating activity in the left and right brain
- Read this dataset, which has been adapted from the StudyForrest project. See Exercise 2 from the NumPy tutorial if you don't remember this dataset!
- Get the mean BOLD response over time, separately for the left and the right brain.
- Plot the BOLD response over time for the left and the right brain.
- You will notice that there is a slight drift in the signal, such that the BOLD response globally increases over time. You can remove this with so-called detrending, using
scipy.signal.detrend(). - Plot the detrended BOLD response over time for the left and the right brain.
- Determine the correlation between the detrended BOLD response in the left and the right brain.
Statistical caveat: Measures that evolve over time, such as the BOLD response, are not independent. Therefore, statistical tests that assume independent observations are invalid for this kind of data! In this exercise, this means that the p-value for the correlation is not meaningful.
You're done with this section!
Continue with Time series >>



